Dec 09, 2023
Problems I Wrote in 2023
...Unlike last year, I posted other stuffs in this year lol.
Compared to last year, I wrote fewer problems. In total, I wrote around 11 problems. Technically, some of them are co-written with someone else, so I couldn't say that I really came up with that many problems. Anyway. Unlike last year, I actually liked some of the problems I wrote this year. In particular, I like Sharing Lapis Talas, Contingency Plan 2 and Count BFS Graph. I will explain later why I like those three.
As usual, I would talk about those problems. Be it the background story on how the problem was developed, solutions, etc. There is no particular ordering on the problems, I just write them here as I remember them.
Enjoy.
CS2040S - Racing Game
Problem link: Here
Editorial: None
To be honest, I didn't plan to set any problems in the practical exams (PE) of CS2040S. However, this dumb me literally said to Steven "oh yeah, I could help in setting PE" at the start of the semester. I completely forgot I said it, until around 1 week before PE. And I was reminded only because PE still need one more problem.
Some might find it weird, but it is actually hard to come up with a good, easy problem. Sometimes, even harder than coming up with a medium or hard problem. And that was exactly the issue we had this semester. The TAs assigned to prepare PE could not come up with an easy problem. Around 1 week before the PE, I joined the group chat for PE preparation. Honestly, I am also bad at designing easy problems. As we were still in the middle of brainstorming, I half-jokingly sent the following message.
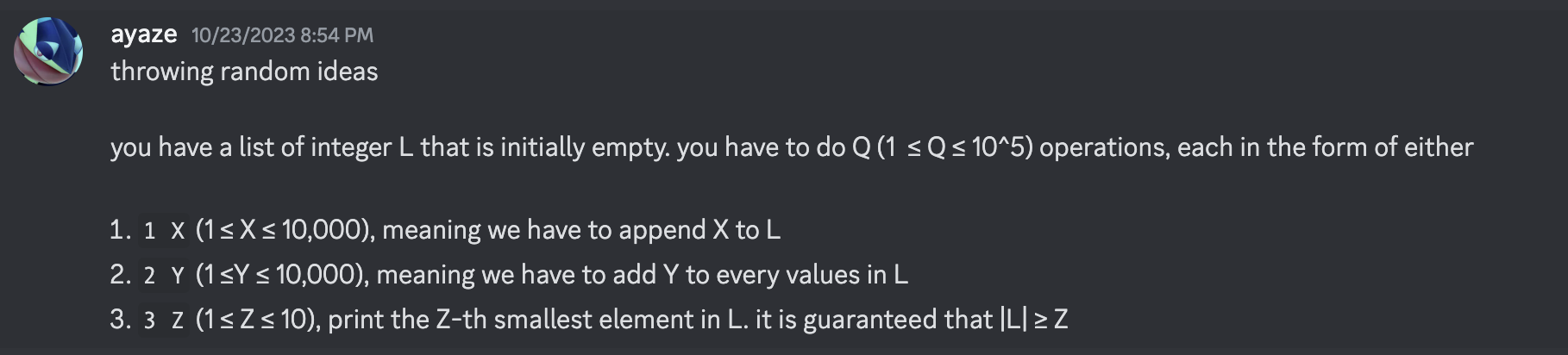
...And somehow everyone agreed to put it in the PE.
Things to note on this problem:
- I consciously set the constraints such that 32-bit integers are sufficient in this problem. I was already tired of students having overflow when they are doing the weekly problemsets.
- I should have bolded the fact that is at most 10.
- It is possible to solve this even without above constraint, but it will be too much for the students.
As Steven most likely will reuse this problem in future iterations of CS2040/C/S, I will not talk about the solution. The only thing I can say if you are struggling with this problem: don't think too much.
CS2040S - One-Punch Wall
Problem link: Here
Editorial: None
After we were done with PE, what comes next is the remedial PE. Again, we were struggling to set the problems :)) I then talked about this with Ammar (for NUS students: he is an ex-CS2040/C/S TA). How this problem was conceived was basically:
> Ammar: How about making a grid with empty cells and walls.
Then, given a starting cell and ending cell, find out whether
there is a path connecting them if we are allowed to break at most one wall.
> Ayaz: Hmm okay, seems too standard. I am also not sure how to make the subtasks.
> (few days later) Ayaz: How about turning this into a query problem?Yes, I listed this problem here just for completeness. My role in setting this problem was only making it more disgusting. I still did most of the problem preparation though.
Things to note on this problem:
- We added an open subtask that can be solved manually. The goal was so Steven do not have to do manual grading anymore (he manually grade submissions with 0 score). Alas, people still ignore the open subtask :|
- The ugly constraint was to ensure subtask cannot be brute-forced in fast language like C++.
As a side note, I am still not sure whether there is solution per query if . Even for , per query is amortized, not in the worst case.
Again, as Steven might reuse this problem in the future, I will not talk about the solution. The only hint I could say is, if you can solve in (after some pre-processing), you are already half-way there.
Gemastik 2023 Final C - Listrik Perumahan
Problem link: Here
Editorial: None, described below
I actually wrote this problem last year. I submitted it to Gemastik, but it was rejected. However, the situation was unclear, at least for me. Do rejected problems get returned to the author? It was not specified in the call for task. I should have clarified this last year when I was a judge there... Anyway, since the situation was unclear and I was too lazy to clarify with the current judges, I just resubmitted the exact same problem to Gemastik. This time, it was accepted.
The problem itself is quite standard if you know Cayley's formula -- the generalized version. We can solve this using inclusion-exclusion, by counting spanning tree which uses some of the missing edges. My intended solution works in .
Gemastik 2023 Final I - Soal Query XOR
Problem link: Here
Editorial: None, I refused to elaborate
If I have to list down my regrets in 2023, writing this problem must be one of them.
I will not elaborate my solution, but some key ideas are:
- Of course, solve each bit independently.
- The implicit array initially will repeat every .
- We can model this into range update-query where we can toggle a range.
Some reasons why I regret writing (and submitting) this problem:
- It is just downright boring.
- The time limit was set insanely tight. I understood that the judges do not want to set very high time limit, but this caused alternate solution (which is slightly slower asymptotic wise) to get TLE.
Next time I have something like this in mind, I will just delete it from my head. Assuming I still actively think of competitive programming problems.
Ideafuse 2023 Qualification D - Twin Subsequence
Problem link: Here
Editorial: None, described below
I actually find this one cute. Although it might be because I rarely write ad-hoc problems. I submitted this problem to Ideafuse because I think it's not that interesting to be submitted to INC or ICPC Jakarta.
I cannot remember how I came up with this problem... But I remember that I was on my way home from Friday Prayer when I first thought of this one. Funny enough, I initially think of a DP solution for this. The DP itself turned out to be useless, and if any, it just serve as my proof on why the greedy solution works.
Now, about the solution. Two key observations:
- The answer is -1 if and only if the characters in the string are distinct.
- Otherwise, suppose there exists such that . Then, we have a twin subsequence .
Thus, we can just greedily look for a pair such that and is minimized. It is possible to solve this in .
OSN 2023 2B - Sharing Lapis Talas
Problem link: Here
Editorial: Will be in the same link as above
I like this problem because it was inspired from my teaching experience. Also, it lets me understand better about a well-known algorithm, in this case Floyd's heapify algorithm
Tracing back, this problem is closely related to what me and Ammar discussed in 2022. Back then, we were TA-ing CS2040C under Steven. Sometimes, when preparing tutorials, we try to think several steps ahead by asking ourselves -- "what kind of weird questions students could ask in the tutorial?" One thing that caught our attention was this particular VisuAlgo question.
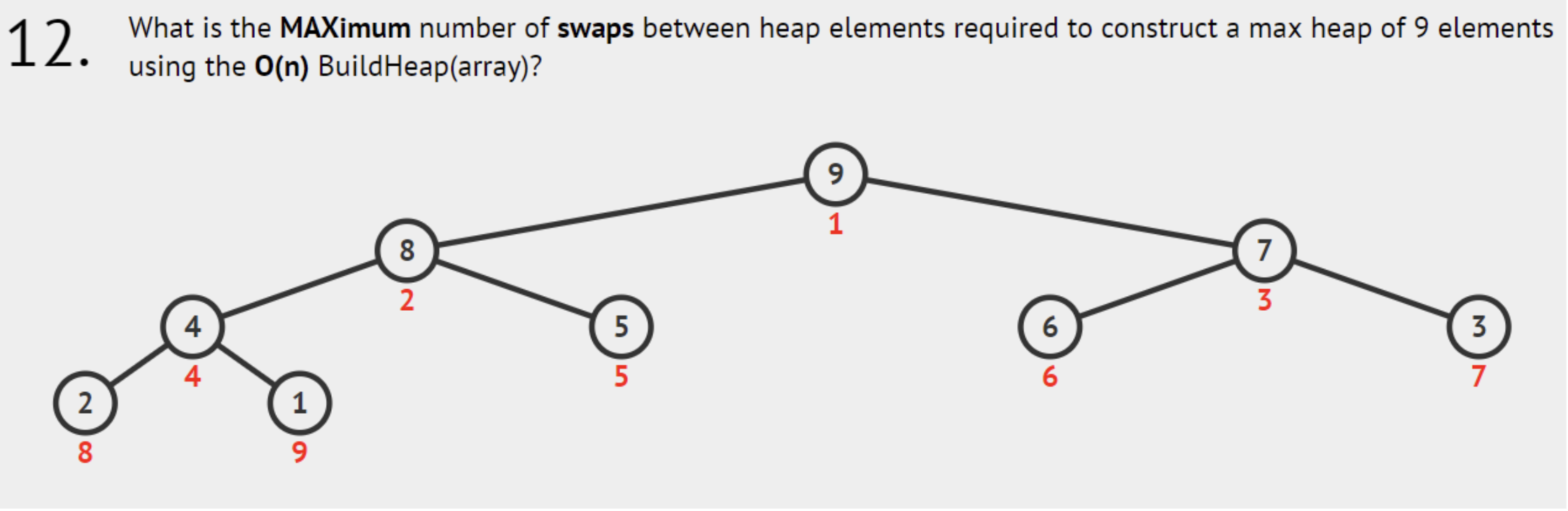
source: trust me bro
It seems plausible that the maximum number of swaps is attained by keep swapping in the direction of the farthest leaf. However, VisuAlgo itself never talked about how to construct an input which attains this. And no, sorted array is not the correct answer.
So yeah, me and Ammar try to think on how to do this. Being a rather technical person, I knew that
we can build a DAG to model the comparison of the initial values in the input and
then apply topological ordering. Being a rather random creative person, Ammar
tried to find a pattern on the input. He did find one, which seems to be the one
implemented in VisuAlgo nowadays.
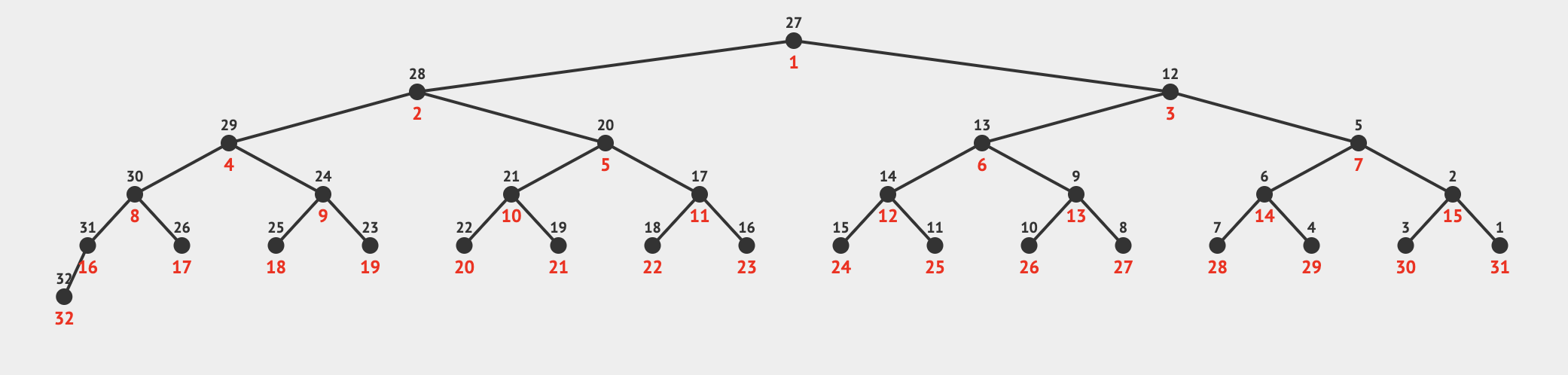
Okay, Ammar has a nice pattern which causes the maximum number of swap. One year later, in early 2023, I was pondering: "if instead of maximizing, we are given a fixed number , can we construct an input with distinct integers such that the algorithm will do exactly swaps?" Well, my idea before (topological sort) already works here. Just in case, I challenged Prabowo to solve this problem. In a few minutes, he replied with the following idea.
initialize ans = N .. 1
for i: N to 1:
pivot = i
while K > 0 and is not leaf:
K -= 1
swap(ans[pivot], ans[leftchild(pivot)])
pivot = leftchild(pivot)...which is simpler, and will also return the correct answer.
Okay, this problem seems to be not that hard then. There is a simple solution, and there is a solution that is a bit tedious but easy to come up with. Back then I was thinking to submit this to Gemastik. However,
Ayaz: "Where do you think I should submit this problem?"
Prabowo: "You know that OSN still don't have enough problem, right?"Yes, this madlad suggested me to submit this to OSN. However, several problems arise:
- The problem seems too easy for OSN.
- It is almost impossible to make several subtasks for this problem.
So we tried to modify this problem. The first thing I tried: "what if we make the input to be not distinct?" But then the tie-breaking becomes tricky. After that, I said: "What if the input is not a complete binary tree?"
This left us thinking for a while, as is now. What I remembered is that there was > 2 minutes silence, meaning this problem might be hard for OSN (Prabowo's bizarre metric). Several minutes later, we noticed that we can tweak his initial idea:
- Instead of trying to swap to the left child, swap to the subtree with the farthest leaf.
- If where denotes the height of node , we will keep swapping until we reach the leaf.
While we did not have a concrete idea in mind, we were confident that we can do everything in . Also, there should be a bunch of subtasks that can be created using this version of problem.
All that is left is to write the problem proposal. However, I felt that something was amiss; There should be an easier solution. That night, I randomly opened VisuAlgo and stared at the pattern that Ammar created one year ago.
...Aha, there seems to be a generalization here.
I noticed that the pattern Ammar found can be explained as the following:
- Decompose the tree into chains. Starting from the root, go to the farthest leaf. Remove every nodes in the chain. Then, do the same thing on the newly created trees until all nodes are assigned to one chain.
- Assign the input such that it is ensured that if a value is swapped, it will be swapped following the chain we have created. This can be done greedily.
- Sort the values in each chain.
It is easy to see that this corresponds to Ammar's pattern. The good thing is, this actually generalizes to any tree! After that, to handle any (not just the maximum), we can play around with the last step; Notice that there is a greedy solution if the tree is just a single chain. We can use this greedy solution on any tree after we decompose it into chains using the way I have described above.
Cool, we have an easier solution now. However, another roadblock appears when I tried to write the problem proposal:
Ayaz: Uhh, how to write the checker?Naively verifying the swap will be , which is in a general tree. I will not talk about this here, as I already write a dedicated blog post for this checker.
Honestly, I like this problem, but writing it was painful.
INC 2023 I - Critical Roads
Problem link: Here
Editorial: Same link as above
"Hey Ayaz, I thought you don't like copy-paste-from-team-notebook problems!"
Yes, I don't like problems which boil down to checking how good your team notebook is. At best, I wanted problems to have extra steps such that we can't solve them if we only use the team notebook as is. Honestly, the extra step in this problem, edge splitting, is not that interesting. So why did I submit this problem?
Well, because the problem I submitted wasn't like this.
In my initial submission, there was an extra constraint: . With this extra constraint, will still be sufficient to solve this problem under 1s. Yes, my initial solution works in that time complexity, and it only relies on some simple observations over DFS.
Now, why the current problem does not have that constraint? A few week before INC, the scientific commitee told me that this problem can be solved for any in using dominator tree. I just checked with them what dominator tree is, and after that, verify whether my reduction from dominating edge to dominating vertex is correct.
They then asked whether it is okay if they bump up the difficulty by removing the extra constraint I mentioned before. Now, my view on this kind of thing: for any problems I have submitted, that the scientific commitee have accepted, they can freely modify them as they deem fit. Even if I dislike their modifications, I will accept their decisions.
So yeah, to re-iterate: I don't like the current version of the problem, but it is fine. I guess, a positive outcome from this problem would be Indonesian competitive programmers are now aware of dominator tree (if they haven't before).
ICPC Jakarta 2023 J - Count BFS Graph
Problem link: Here
Editorial: Same link as above
At this point, writing "given this pseudocode, analyze something about it!" problem has become a tradition for me. Personally, I like this kind of problem if the pseudocode is something that is well-known (like in this problem) or looks like something that we will come up naturally at some point (like in Greedy Knapsack). So yeah, I like this problem because it analyzes BFS which is well-known in Computer Science.
Initially, the setting was not BFS. Instead of BFS, what I tried to tackle was DFS. After spending several days without anything useful, I think, "what if we do BFS instead?" Because I spent several days working on DFS, somehow, I overcomplicated my solution. At first it was a weird , before I realized "oh, it can be solved in ".
During ICPC Jakarta, I thought it was easier than problem H which is also another counting-with-DP problem. However, judging from the final scoreboard, I might be wrong.
There are two things that I am still interested in, related to this problem.
- Can this problem be solved in ?
- Can we solve the DFS-variant (the initial problem) in polynomial time?
ICPC Jakarta 2023 I - Contingency Plan 2
Problem link: Here
Editorial: Same link as above
Writing this problem was a humbling experience for me. I started with a strong claim, realized it was wrong, then weaken it. Repeat this for several times. Now I know that whenever I think my idea is correct, most likely it is not.
If I remember correctly, back then, I was reading this paper (or other paper, but it follows the same line of work). While trying to understand the paper, one thing that came into mind: "how to make a total ordering of the blocks?". Given that the graph is a DAG, the follow-up I had was "what is the minimum number of edges I need to add such that the graph is still a DAG and total ordering exists?"
After that, I read the Wikipedia page of topological ordering (for no actual reason). One thing that caught my attention is basically
A DAG has exactly one topological ordering if and only if it has a hamiltonian path.
It is not instantly clear to me why this is correct, though it makes sense after reading the proof. And now I feel stupid.
Okay, seems useful. This directly translates into a lower bound: find the minimum path cover (MPC) of the graph and "glue them". Thus, the lower bound of the edge we need is . Then I start with a pretty strong claim.
Claim: Any MPC can be ordered such that we can add edge between adjacent path, which preserves acyclicness and induces a hamiltonian path.
If this claim is true, then we are done as this match the lower bound. However...
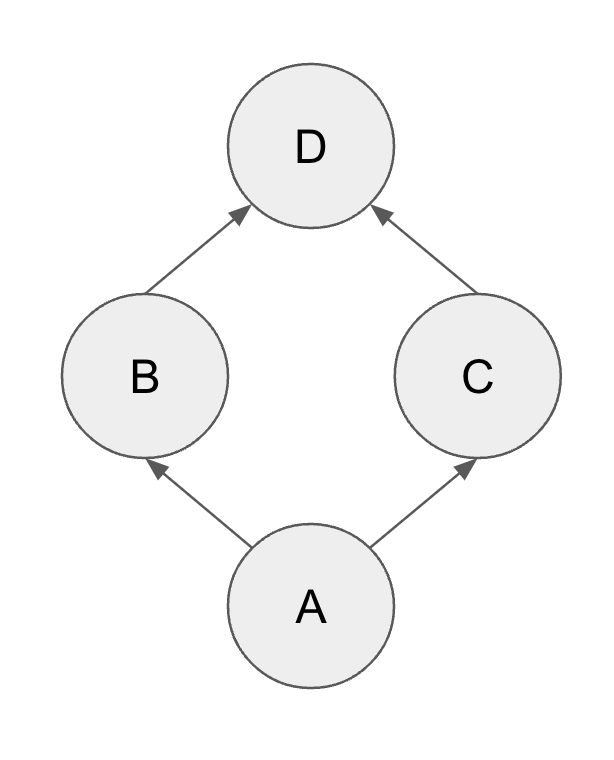
Notice that in above graph, a possible MPC is and . However, as you might notice, there is no way to "glue" the paths such that the new graph remain acyclic. Okay, I screwed. But then, I noticed that another MPC admits "glue": and . Thus, I weaken my previous claim.
Claim (Fixed):
AnyThere exists MPC which can be ordered such that we can add edge between adjacent path, which preserves acyclicness and induces a hamiltonian path.
Now this seems correct, but this brings a headache. How do I find that particular MPC? Fortunately (or unfortunately?), this claim is also wrong. I was reading Dilworth's Theorem when I stumbled upon this graph.
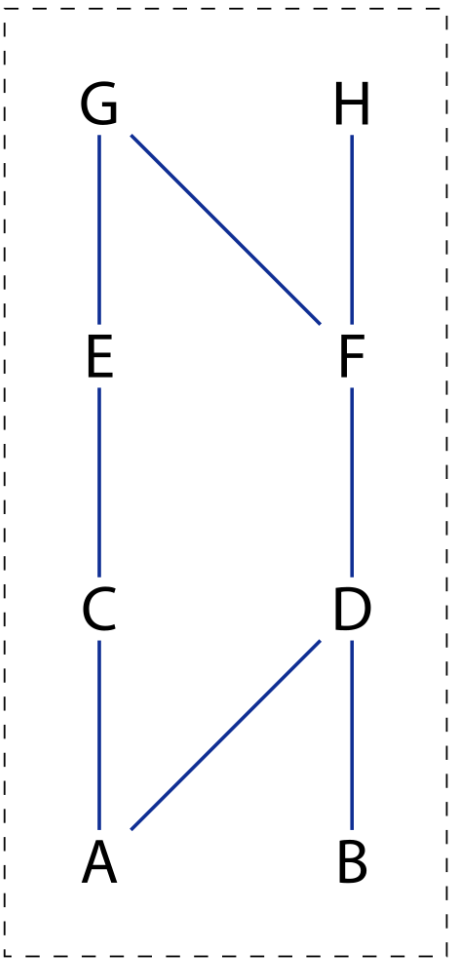
If we direct the edges upward, notice that there is one unique MPC: and . However, it is impossible to "glue" them.
Okay, my claim is still wrong. Can I somehow fix this? Maybe if I only consider a special type of graph? As it turns out, we can always find a way to "glue" if the initial DAG is a polytree.
Claim (Fixed Fixed): On polytree, any MPC can be ordered such that we can add edge between adjacent path, which preserves acyclicness and induces a hamiltonian path.
Fun fact, I only learned the term polytree during this year, and it was because some fellow PhD students researched about learning in which polytree is commonly used.
So yeah, I have to weaken my initial claim several times before I reached the current version. Truly a humbling experience, I will never trust anything I claim anymore.
By the way, a few weeks before INC, I found this question on StackExchange. It is basically asking similar thing, and the answer there is very similar to the solution of this problem. However, the answer there claims to work for any DAG, which I doubted. Anyway, if it is similar to my solution, this means it will also work for polytree. Also, this means the answer is google-able. I already raised that this StackExchange post existed to the scientific committee. In the end, they decided to keep this problem to be used in ICPC Jakarta because finding that post is not that trivial, plus their claim could be incorrect.
Regarding this problem, I am still wondering whether it is possible to solve this in polynomial time if the input graph is any DAG, and not just a polytree. As for now, my hunch told me that it is not possible. However, I have a severe skill issue so this could be wrong.
Unused - Twin XOR
Problem link: None
Editorial: None, hinted below
Unused because this is very classic. I still find it as a nice exercise though.
The problem:
You are given an array () of size (). Find two disjoint subsequences with equal XORs. If there are multiple solutions, output any. If there is none, output "-1".
The problem itself is not that hard. Anyways, below are hints to solve this problem.
Hint 1
We can always construct a valid answer from two subsequences (not necessarily disjoint) with equal XORsHint 2
Using Hint 1 and pigeon hole principle, what is the minimum N which guarantees that solution always exist?Hint 3
Use the bound from hint 2 to prune the array. Then, find the solution using meet-in-the-middle or Gaussian elimination.FYI, the main motivation of writing this in this post is because it is closely
related to the next problem -- Deck-Building Game AKA Twin XOR Count.
ICPC Jakarta 2023 K - Deck-Building Game
Problem link: Here
Editorial: Same link as above
AKA Twin XOR Count in my notes.
I will start by saying this: I have no idea how FWHT works. I only know that it can be used to XOR convolute two polynomials in where is the degree of the convolution result.
Let's start with how this problem was invented. A few months ago, I challenged
Suhendry to solve Twin XOR. Weirdly, he was unable to solve it. I should
have realized something is wrong earlier, as it is impossible for him
to not solve it. A few days after that, I discussed Twin XOR with him.
At some point, I noticed that we were not on the same page. After clarifying here and there,
I realized that he misunderstood the problem: instead of constructing the two disjoint
subsequences, he tried to count how many ways we can construct such subsequences.
Thinking for a bit, I realized that I could not solve this either. So I spent several hours worth of commuting thinking about the counting version. Sadly, still nothing useful. At best, I know I can model it as "find the coefficient of from " (think of as the XOR convolution). I tried solving it for instead of , but I'm still stuck.
At night, I decided to shower. Sometimes, I get really nice idea while showering, I don't know why. Hence, again I ponder about this problem.
"Non-zero coefficients of will be on , , , and "
"Non-zero coefficients of will be on , , , and "
"What will I get if I combine them?"
" to "
"....."
"?"
"Seems the span will form two contiguous sequences if I do divide and conquer over the convolution?"
To be honest, I didn't formally prove it but I was convinced that this is correct. Formally proving it shouldn't be that hard, it is just playing with the bits as DnC will split the recursion based on the most significant bit. I quickly finished showering and try to write a proof of concept. Here is what I wrote that night. Note that for simplicity, the proof of concept assumes the elements of to be distinct.
To be honest, I like this idea as I can treat FWHT as a black-box (really, what I need is just an algorithm to do XOR convolution efficiently). When the scientific committee worked on preparing this problem, they also couldn't find a better solution. Sadly,
- There exists a solution that doesn't require the DnC, as mentioned in this CodeForces comment. To be honest, both me and Prabowo still do not understand this idea. To be frank, as I mentioned at the start, I have no idea on how FWHT works.
- Also mentioned in the same CodeForces blog, the same problem has appeared several years ago. I felt that this might be the reason why there are more ACs on this problem in the mirror, despite me and the scientific committee thinking that this problem is pretty hard.
Welp, again I was reminded that whatever I wrote, most likely someone has already written it somewhere else.
Nevertheless, I am still curious whether it is possible to solve this problem more efficiently -- perhaps something like ? Albeit this does not seem plausible.
Afterwords
Somehow this post is longer than I initially expected. Doesn't matter, I rarely post in this blog anyway.
I guess that is all for problems that I wrote (and published) this year. There are hiccups here and there, but overall I am quite satisfied.
Now, I'm not planning to write any new problem next year, and this might continue for indefinite time. I might still submit some problems, but they are from my stash of unpublished problems. Several reasons why I want to take a break:
- I just want to take a break and do other things instead.
- With my knowledge stuck in 2015-2019 era, I don't think I am that up-to-date with recent techniques.
- Nowadays, I rarely do competitive programming. I felt that the problems I write recently are not that relevant to the current meta. Also, it is likely that I am not aware if the problems I wrote have appeared in another contest. I do try to google them before submitting, but it could be that my google-fu isn't that good.
I also hope that more people (esp. younger ones) submit problems to ICPC Jakarta. If you read ICPC Jakarta 2023 Editorial, you will notice that most of the problem authors are... pretty old. The youngest there are from my TOKI batch (me + Prabowo + Rafael + Xing-Xing), TOKI 2015. Old, in my standard. Also, the authors in ICPC Jakarta rarely do competitive programming now, except for Prabowo (I think). It will be nice if there are problem authors who still actively do competitive programming, so we have authors who are more up-to-date with the current trend in the competition.
Let me retire
