Ayaz' Home Page

In the recently concluded OSN (yes, I prefer to call it OSN instead of Indonesian NOI), there was one problem authored by me and Prabowo. It is a constructive problem called Sharing Lapis Talas. I rarely write constructive problem, but when I do, usually the custom checker is not hard to write. Most of the time it is just simple checking based on what the problem is about. In this blog, I will talk about the checker for this problem, which is way harder than the problem itself.

I will also talk a bit about this problem. Hence, if you have not read the problem or still trying to solve it, be warned that from this point onward, I might spoil the problem for you. Here is a lapis talas so you don't get spoiled.

Okay, I assume everyone who get through that lapis talas is okay with being spoiled.

First, let me describe the abridged problem statement.

Given a rooted tree with $N$ nodes, find the initial values stored in each node such that Floyd's heap construction (modified to build a min-heap) will do exactly $K$ swaps.

So, the checker will read the initial values, then check whether Floyd's heap construction will do exactly $K$ swaps or not.

Now, you might say "isn't Floyd's heap construction runs in $O(N)$? So the number of swaps will also be $O(N)$?" That is true if the tree is a complete binary tree. However, in this problem, the tree can be anything. Floyd's heap construction may swap up to $O(\sum_{i=0}^{N} height(i))$ times. Thus, for trees that are very tall, for example a line graph, Floyd's heap construction may swap up to $O(N^2)$ times.

If we only aim to build a correct algorithm, then it is pretty easy: In each node, maintain a BBST to store the values of its children. Then, in each step of the algorithm, we can easily check whether we need to swap with one of the current node's children in $O(\log{N})$. Thus, the time complexity of this algorithm will be $O((N + K) \log{N})$.

Okay, we have a correct algorithm. However, it is too slow; Recall that $K$ is $O(N^2)$. Assuming $N \le 100\;000$ (as otherwise this problem is pretty easy to solve), checking one test case may take several seconds. The technical committee will kill us if we use this checker.

So let's think of a better way to solve this. First of all, instead of talking about min-heap (which this problem is about), I will assume we are dealing with max-heap instead as I found it easier to think about. Note that if we can solve it for max-heap we can also solve it for min-heap. Usually, this involves minimal amount of work, for example by multiplying each value with $-1$.

Now, as with several problems related to paths in tree, the very first idea I tried was to use heavy-light decomposition (HLD). Note that this HLD is a bit different with the original HLD; here, a heavy child of node $v$ is defined as the largest child of $v$ (with some tie-breaking). Meanwhile, in the original HLD, the heavy child of $v$ is node $w$ such that $w$'s subtree size is at least half of $v$'s subtree size. Then, we can decompose it into several heavy paths, where a heavy path is a maximal path connecting heavy childs. A good thing about this HLD variation is that it is ensured that a heavy path will always go all the way into one of the leaves of the tree.

Okay, how to use HLD here? First, let's see the basic property of Floyd's heap construction.

Property 1: Suppose right now the algorithm is in the $i$-th iteration (i.e. starting to heapify from node $i$). Then, all subtrees rooted at node $j > i$ will be a max-heap.

How can we use above property? Well, Property 1 implies that in every heavy path, nodes that have been processed (i.e. all node $j > i$) will have values sorted in ascending manner from leaf to the top. This looks pretty useful.

Notice that in our swapping process, there are two cases:

1. We stop in this heavy path. That is, our swapping process swaps down until we reach a node, where either all of its children values' are smaller or it is a leaf.
2. We moves into a new heavy path. That is, there is a node $v$ in the heavy path which sibling, $w$, has bigger value than $v$. Thus, we move into $w's$ heavy path.

By the guarantee of HLD, 2nd case (moving/switching to a new heavy path) will only happen $O(\log{N})$ times. Thus, if we can process each case in $o(N)$ time, there is a chance for a checker with time complexity of $o(N^2)$!

By the implication of property 1, the 1st case can be handled in $O(\log{N})$. How? We can maintain a BBST in each heavy path, storing values of node that have been processed. Say our value is $x$. The 1st case can be done by finding the highest value which is less than $x$. Furthermore, the number of swaps will be $(\textrm{number of processed node here} - \textrm{number < x})$. $\textrm{number < x}$ can be found in $O(\log{N})$ via rank function of BBST, which is also supported in some C++ compilers. Also, at the end of case 1 we need to insert one value into the BBST, which again can be done in $O(\log{N})$.

Good, we can solve case 1 in $O(\log{N})$. However, how to solve the 2nd case?

We can maintain another BBST in each heavy path, this time to store the nodes such that it has a light child (child which is not the heavy child) with bigger value compared to its heavy child. Everytime we finish a swapping in a heavy path, we update this BBST. It can be shown that over the course of Floyd's heap construction, there will be $O(N)$ insertion and removal over all BBST. Hence, overall, the time complexity will be $O(N \log{N})$ to do update in this case.

Finally, to combine the 1st and the 2nd case, we need to check which happens first: the stopping, or switching to another heavy path. There is some technicality involved here, but it can be resolved by also storing the node's height within all BBST, not just its value or the node's identity.

Well, seems we are actually done here, right?

Do we?

Cause if we are, I will not be writing this blog.

Notice that there is a hole in the 2nd case's idea: While it might be true there are $O(N)$ insertions and removals, we cannot know whether such thing happen unless we inspect all nodes in the swapping path. At worst, we might inspect $O(N)$ nodes without doing any insertion and removal. Thus, the time complexity of this idea will be $O(N^2)$.

Fun fact: when we submitted this problem, the checker we described had this issue. Took me one good sleep to finally come up with a correct and fast enough checker for this problem. This is also why I wanted to write this blog, as it turns out that the checker is not trivial :)

Okay, this idea does not go well. Can we somehow fix this? Can we find a faster way to insert and remove things, and find the topmost node in which a switch might occur?

Yes we can! To do that, we need to rely on the following claim.

Claim 2: Suppose that we switch to a node $w$, where its sibling in the heavy path is $v$. Denote $h(v)$ as the number of $v$'s descendant in $v's$ heavy path including $v$ (we can view this as $v$'s height in the heavy path). Denote $x$ as $w$'s value. Then, there are exactly $h(v)$ nodes in $w$'s heavy path with value smaller than $x$.

Proof Sketch: First, denote the number of nodes smaller than $x$ in $v$'s heavy path as $k$. We split into three cases.

1. $k < h(v)$. By property 1, these must form the $k$ lowest nodes in the heavy path. As $k < h(v)$, this implies $v$'s value is bigger than $w$'s value, in which a switch should not occur.
2. $k = h(v)$. This implies $v$'s value is smaller than $w$'s value, so a switch should occur.
3. $k > h(v)$. I will omit some details but the main idea is that this implies the value in $w$ (and $v$)'s parent is smaller then $w$'s value, which contradicts property 1.

Thus, the switch can only happen if $k = h(v)$.

Now, how can we use above claim to help us? Suppose we have a data structure that supports all of the following operations on an array $A$ in $O(\log{N})$:

1. Add $A[l \dots r]$ $(1 \le l \le r \le N)$ with a value $x$.
2. Set $A[i]$ $(1 \le i \le N)$ with a value $x$.
3. Report any index $i$ such that $\min(A) = A[i]$.

Then, we can handle the second case in $O(\log{N})$.

To see how to do that, first, let's commit a war crime by abusing many notations. Let $h(v)$ be the "height in heavy path" as described before, except that $v$ here is value $v$ instead of node $v$. Here, we take the height of the sibling of node storing $v$ as $h(v)$. Then, let $l(v)$ be the number of nodes in the heavy path with value less than $v$. We will use the aforementioned data structure to maintain $h(v)-l(v)$ over all $v$ which are values of a light child connected to this heavy path.

Say we have processed all $i \ge 3$. Then, the following is an example of the state of the tree and the corresponding state of the data structure. For simplicity, we define the $h(v)-l(v)$ of values that do not exist as $\infty$.

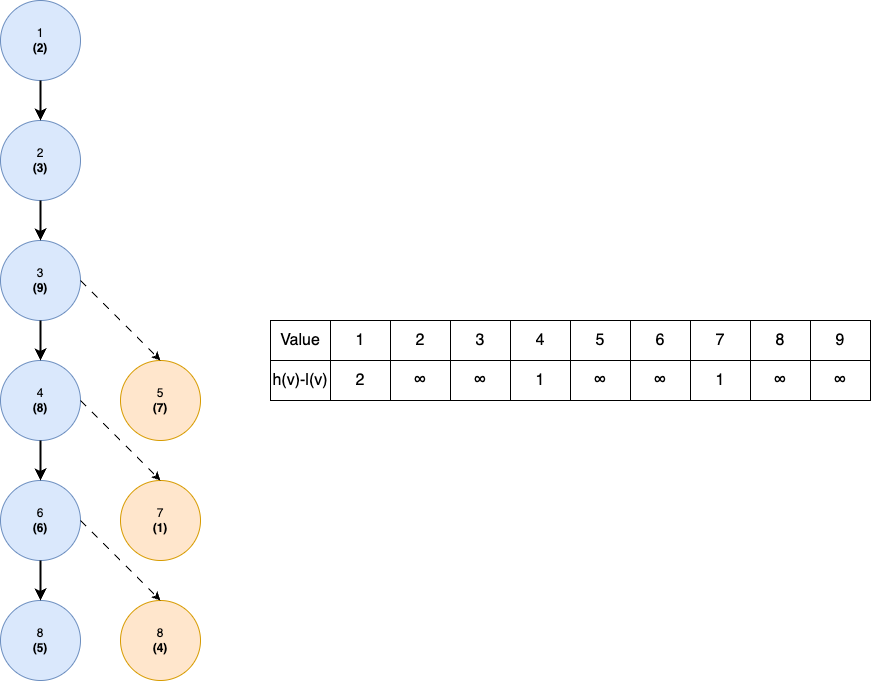
To understand the picture, we see that there are 3 light children: 5 with value 7, 7 with value 1, and 9 with value 4. For value 7, $h(7) = 3$ as 5's sibling, 4, has a height in heavy path of 3. Then, $l(7) = 2$ as there are two values less than 7 in the heavy path. Thus, in the data structure, we store $h(7)-l(7) = 3-2 = 1$. The same idea is also applied to value 1 and 4.

Now, let's say that we process $i = 2$. It can be verified that the tree will look as the following after we are finished with $i = 2$. Red color denote the affected nodes and values in the data structure.

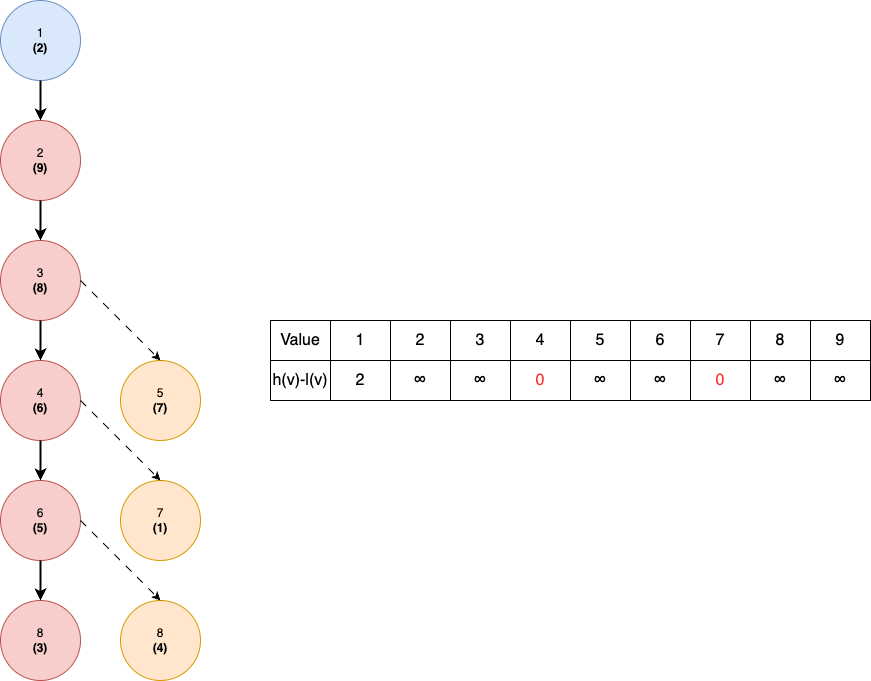
Let's continue with $i=1$. Now, interesting thing happens. Remember that our switching condition is basically $h(v) = l(v)$. As we store $h(v)-l(v)$, this corresponds to $h(v)-l(v) = 0$. We can see that in the data structures, indeed that values $v$ such that $h(v)-l(v) = 0$ is a potential candidate for the switch. In particular, value 4 and 7. In this case, as the one with value 7 is higher up in the tree, we will switch into that one. The following illustrates what happen after we do $i=1$.

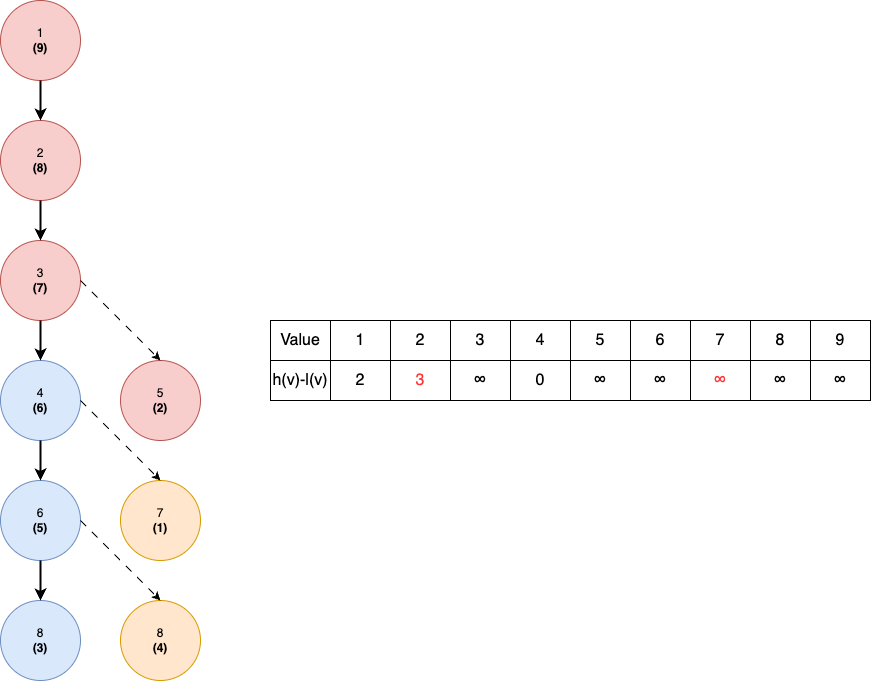
Okay, we have seen the data structures in action. To understand how to use the operations in the swapping process, recall that we can see this swap as an insertion and a removal. Then,

• If we insert a value $v$ into the heavy path, we add $A[v \dots N]$ by $-1$.
• If we insert a value $v$ as the value of a light child, we set $A[v] = h(v) - l(v)$.
• If we remove a value $v$ from the heavy path, we add $A[v \dots N]$ by $1$.
• If we remove a value $v$ as the value of a light child, we set $A[v] = \infty$.
• To see whether a switching occur, we can do operation 3 and see whether the returned index $v$ have $h(v)-l(v) = 0$.

Finding $h(v)$ is pretty simple with some precomputation. Meanwhile, $l(v)$ can be done using BBST we described in case 1. Now, you might notice that to find the topmost candidate such that switching might occur, operation 3 is not enough. It is not enough, but there are some simple modifications to handle that:

• Instead of only storing $h(v)-l(v)$, we also store $h(v)$ which then can be used for tie-breaking.
• Instead of returning any index, we return the maximum index.

Oh, I have not talked about what data structure that can be used here, right? Well, we can use a (self-written) BBST or a dynamic segment tree. Personally, I prefer to write dynamic segment tree as it is easier to implement.

That is pretty long, but we are done! With above idea, we can handle the 2nd case in $O(\log{N})$. Thus, both 1st and 2nd case can be handled in $O(\log{N})$ per heavy-path. As HLD guarantees we will go through $O(\log{N})$ heavy paths, the complexity of handling a fixed $i$ is $O(\log^2{N})$. Hence, we now have a checker with time complexity $O(N \log^2{N})$, that is independent of $K$. Yay!

You can check the proof-of-concept I wrote here. Note that it might be not that reader friendly as I intended it only as a proof-of-concept.

Actually, it is rare for me to try to code nowadays. When I submit a problem to a contest, unless they ask me to, I rarely code solution, testcase generator, etc. I only wrote the proof-of-concept here because I was paranoid that the idea above is wrong somewhere. You can see that in the proof-of-concept I also stress-tested it on some small trees. Back then, after I coded the proof-of-concept, I sent it to the scientific committee for them to try it.

Actually, I still do not know how the checker that the scientific committee of OSN wrote works. Considering the OSN only recently concluded, I think it will take some time before they uploaded it into GitHub. Hocky did mention that their checker runs in $O(N \log^2{N})$ time, though I still do not know how. I do hope that their checker is simpler than the one I wrote here though :') Update: okay, they have uploaded it in GitHub. I still don't have time to fully understand it, but my impression is that it also uses HLD, but instead of simulating the "shifting down" process, they try to "move things up" from the largest value. Looks more simple :)

To conclude this post, I want to say that the checker of this problem is actually a hard problem on its own. Although, I prefer not to have it in a contest because well... coding it can be pretty nasty XD Nonetheless, I found the experience itself to be a fun one. It just feels satisfying when I realize that a relatively simple claim (Claim 2) leads to a logarithmic solution for the hard case :)

See you in the next post!